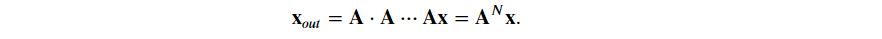Weight Initialization is the most underrated concept in the deep learning terminology. I have seen many newbie deep learning practitioners and even some experienced ones ignoring this important concept. Unlike some already available tutorials or blogs, we will not talk about why you should not initialize your weights with all zeros or all ones rather I will give a different perspective to weight initialization using eigenvalues and eigenvectors.
Note: This post assumes readers to have basic familiarity with eigenvalues and eigenvectors.
Basic Notations :
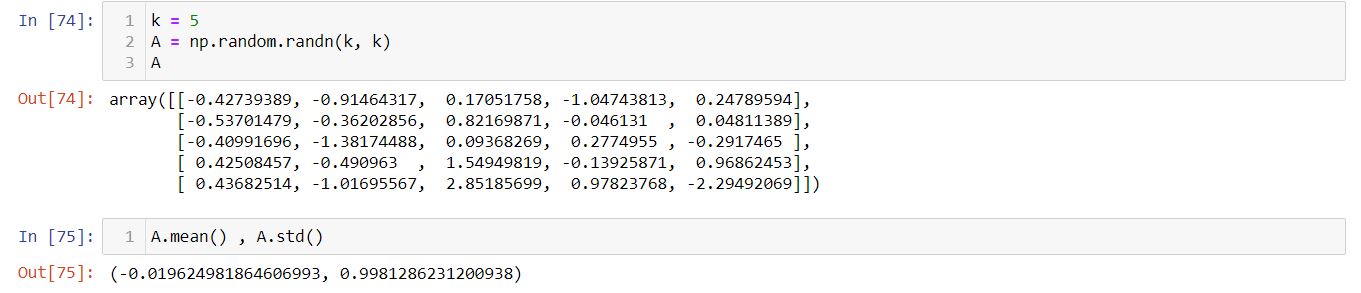
- A: a random matrix whose entries are standard gaussian distributed of dimension (k,k).
- x: a random gaussian vector of dimension (k,1).
We can think of a neural network as a stack of many layers where each layer does a linear transformation followed by a non-linear operation using a function commonly known as activation function. To keep this post simple and easily understandable, I will focus only on the linear transformation part.
The linear transformation part in our case is basically a repeated matrix operation A which can be written as:
To start with we will take the value of k as 5 and randomly initialize the matrix A with standard Gaussian.
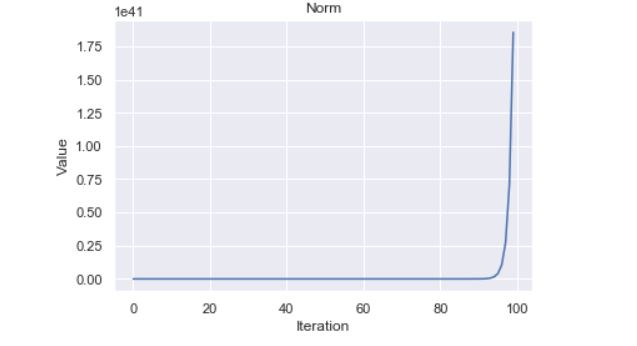
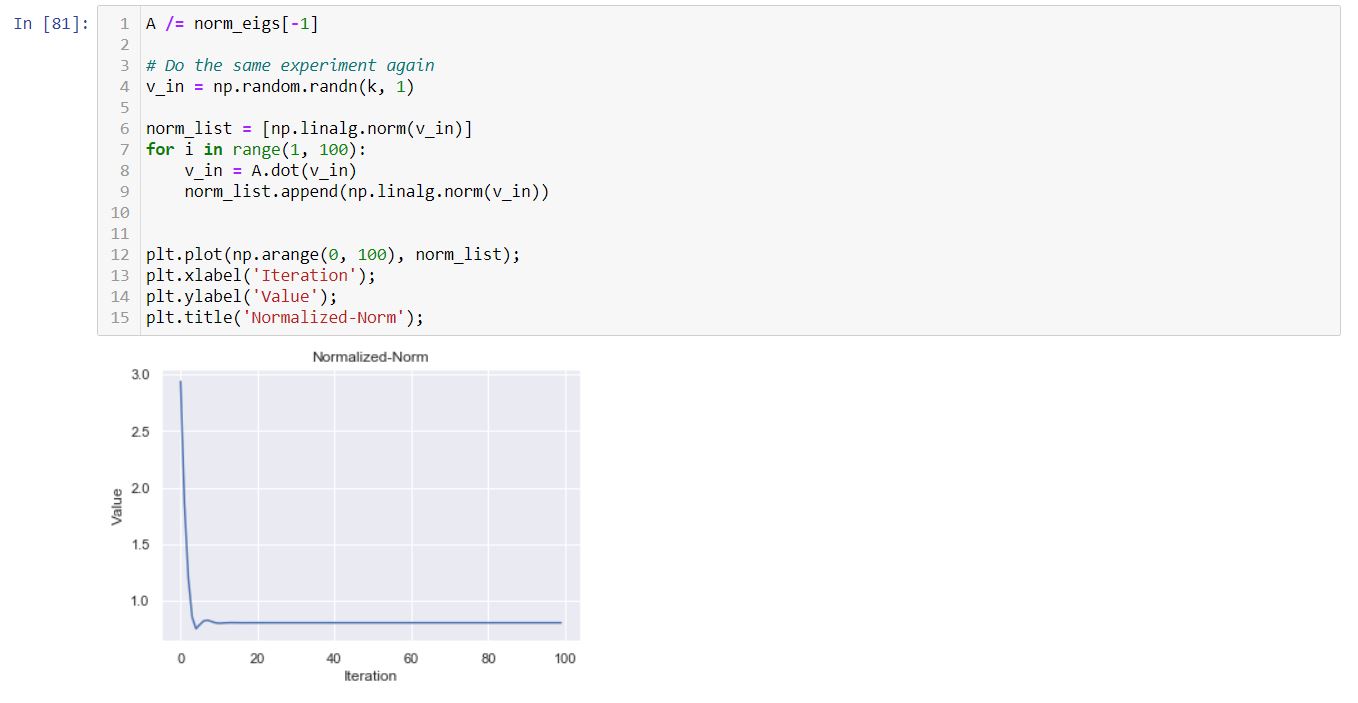
Let us now analyze the repeated multiplication and plot the norm.
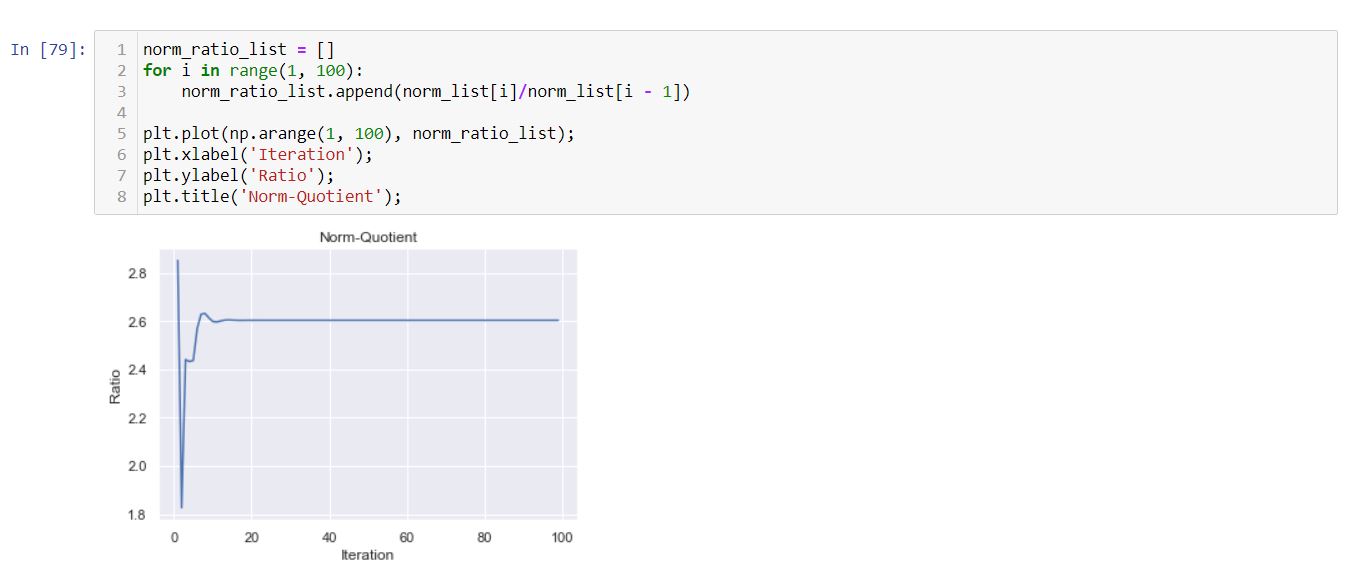
From the graph, we can easily observe that the norm of the matrix is exploding. Let’s check the consecutive norm ratio a.k.a quotient and see.
The quotient is getting saturated after some iterations to a specific value approximately 2.60… which let’s call as stretching factor of our matrix. If you recall in linear algebra there is a very important concept of eigenvalues and eigenvectors.
From wikipedia: an eigenvector or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue is the factor by which the eigenvector is scaled.
Let’s see the eigenvalues of the our matrix A
The largest eigenvalue is approximately equal to our stretching factor, is this an error or just a coincidence! Well it is not.
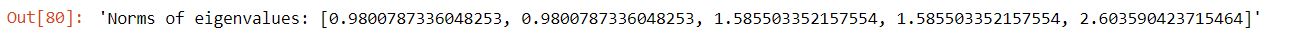
Microscopic view
Our random vector x points in every direction so in particular, it also points in the direction of the principal eigenvector. When the matrix A is applied, this vectors stretches in every direction including the principal eigenvector direction. The repeated application of A will make this random vector aligned to the principal eigenvector until our random vector gets transformed into the principal eigenvector. This is known as the Power Iteration method of finding the largest eigenvalue and eigenvector.
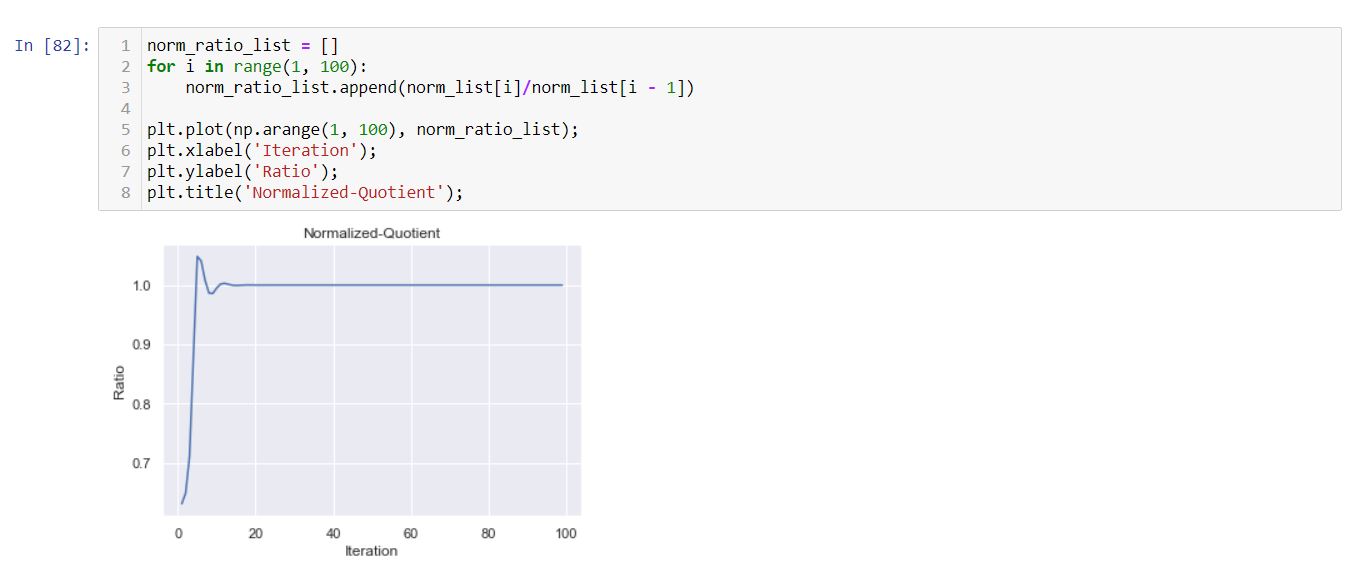
But how this solve our problem of the values exploding? Well, let us see what happens if we normalize the matrix A with the largest eigenvalue and plot the norm again.
Similarly let’s plot the norm ratio again.
After normalization, the problem of exploding is rectified and gradually stabilizes at a specific value. This eigenvalue concept of a random matrix is of great importance in proper weight initialization of deep networks.
Summary
In this post, we have seen that eigenvalue and eigenvector play a crucial role in the initialization of a matrix. This concept is directly applicable to the proper weight initialization of neural networks. In the next post, we will see about Kaiming and Xavier’s initializations.
References:
- https://www.d2l.ai
- Van Loan, C. F., & Golub, G. H. (1983). Matrix computations. Johns Hopkins University Press.
- I am sure I would have borrowed ideas from other sources as well and I apologize if I missed acknowledging them.
Cheers,
Shreyans